Author: Jinhang Jiang

Student Researcher at ASU Actionable Analytics Lab

Image by Author

Word2vec (published by a team of Google researchers led by Tomas Mikolov), as a “breakthroug technique” in the natural language processing field, has been eight years old. They pioneered the concept of word embedding as the foundation of the technique.

So far, the use of embedding has been applied to a wide range of analyses and has had a significant impact. Many concepts in machine learning or deep learning are built on top of one another, and the concept of embedding is no exception. Having a solid understanding of embedding will make learning many more advanced ML techniques much easier.

Therefore, in today’s blog, I’ll guide you through the following topics to help you gain a thorough understanding of the definition and applications of embeddings:

1.Embedding: A Task-Specific Dictionary
2.Why We Want Embeddings
3.The Various Applications of Embeddings
4.Summary

Embedding: A Task-Specific Dictionary

From Google’s Machine Learning Crash Course, I found the description of embedding: An embedding is a relatively low-dimensional space into which you can translate high-dimensional vectors. Embeddings make it easier to do machine learning on large inputs like sparse vectors representing words. Ideally, an embedding captures some of the semantics of the input by placing semantically similar inputs close together in the embedding space. An embedding can be learned and reused across models.

That’s fantastic! That is probably the most precise and succinct description of embedding I could find online. Nonetheless, it is still a little perplexing and vague. So, how can we explain it in layman’s terms when pretending to have just a rudimentary understanding of machine learning?

Here is an example: when applied to a text mining project, embeddings can assist us in learning the semantic meaning of a word by studying what other words it often appears next to. Then we can produce a list of embeddings, which can be treated as a task-specific dictionary. If you want to learn more about a particular word in your corpus, go to the “dictionary” and look it up. However, instead of providing you with the human language definition, it will return a vector of numerical values to reflect its semantic meaning. Furthermore, the distance between those vectors measures the similarity and relationship between the terms in the project.

Image by Author

As you can tell from the name of word2vec - “word to vector,” which turns a word into a vector of numbers. In other words, embedding is a string of numbers that serves as a unique identifier. We can use the embedding technique to assign a unique numerical ID to a word, an individual, a voice sound, an image, etc. in your research. Scientists, using this idea, have created many fascinating 2vec-style models to facilitate the machine learning process. I will show some of them in the 3rd session.

Why We Want Embeddings

Here are several reasons why we want to include embeddings in our project:

First, current machine learning models continue to favor numerical values as inputs. They are similar to math nerds in that when fed numbers, they can quickly capture vital information but are slow with discrete, categorical variables. However, when researching computer vision or voice recognition and the like, we are unlikely to be able to collect or only collect numerical data for our targets/dependent variables. Converting such discrete, categorical variables to numbers can help with model fitting.

Image by Author

Second, it helps reduce dimensions. Someone may argue that the one-hot-encoding technique is how we handle categorical variables. However, in today’s data science world, it has proven to be much less effective.

When dealing with a variable with four distinct types, we will usually create four new dummy variables to cope with it. Moreover, it has previously worked well.

Yet, consider the following scenario: we are researching consumer feedback for three products. We would only have one variable for each observation — the review content. We can build a term-document matrix and then put it into a classifier or some other types of models. However, let’s suppose we have 50 thousand reviews for each product, and the number of total unique words in the corpus is one million. Then we will end up with a matrix whose shape is (150K x 1M). This is a ridiculously large input for any model. And that is when we need to bring in the idea of embedding.

Assume we reduce the dimensions to 15 (a 15 digits ID for each product), take the average of the embeddings of each product, and then colorize them based on the numerical values, this is what we got:

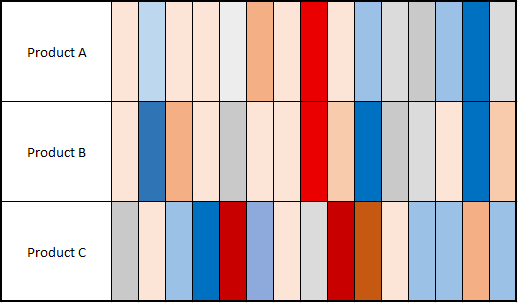
Image by Author

Even though there is no human language presenting, we can still perceive that customers talk about products A and B more similarly than product C. And this matrix’s shape is only (3 x 15).

Here is another example talked about on Google Machine Learning Crash Course, talking about how to use embedding for a movie recommender system: Embeddings: Categorical Input Data.

The third reason is to reduce complexity. It is kind of like the extension of the second reason. Embedding also can help translate the very complex information into a vector of numbers. Here is an example in social network analysis:

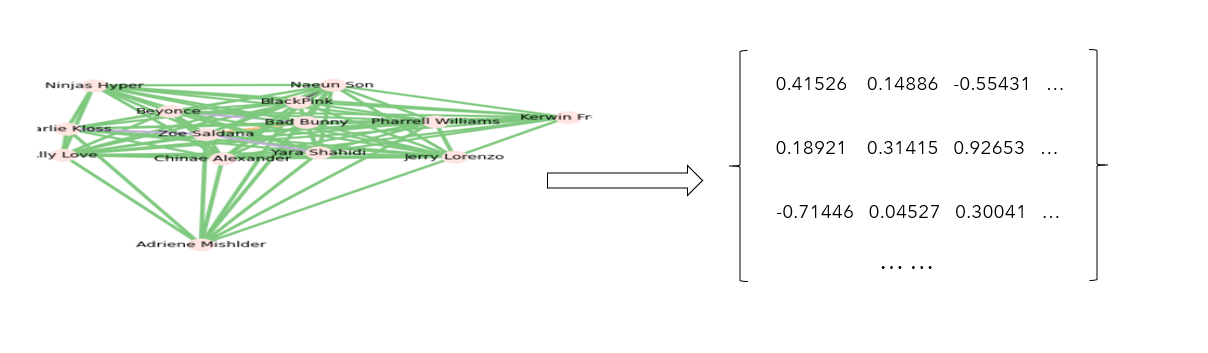
Image by Author

Initially, we collected the data from social media and converted it into a social network analysis graph. In the graph, we can use the distance between the nodes and the color of the ties to interpret the similarities between the nodes. However, it is complicated and hard to read. Right now, we only have 14 nodes in the graph, and it is already a mess. Can you imagine what happens if we were to investigate 100 nodes? This is referred to as complex (high-dimensional) data. However, by using certain techniques to aid in dimensionality reduction, we can transform the graph into a list of embeddings. As a result, instead of the jumbled graph, we now have a new, clean “dictionary” for the nodes. We can use the “dictionary” to make a human-readable visualization.

The Various Applications of Embeddings

You must have been excited to see some applications of embedding in practice after discovering what it is and why we want it. So, I selected a list of interesting applications using the idea of embedding along with some related literature or usage demonstration.

Natural Language Processing:

word2vec:

• Paper: [https://papers.nips.cc/paper/5021-distributed-representations-of-words-and-phrases-and-their-compositionality.pdf]
  
• Explanation: [https://jalammar.github.io/illustrated-word2vec/]
  

sent2vec:

• Paper: [https://arxiv.org/abs/1703.02507]
  
• Explanation: [https://bit.ly/3uxFJ7S]
  

doc2vec:

• Paper: [https://cs.stanford.edu/~quocle/paragraph_vector.pdf]
  
• Demonstration: [https://towardsdatascience.com/detecting-document-similarity-with-doc2vec-f8289a9a7db7]
  

Image Analysis:

Img2vec:

• Explanation and demonstration: [https://becominghuman.ai/extract-a-feature-vector-for-any-image-with-pytorch-9717561d1d4c]
  

Social Network Analysis:

node2vec:

• Paper: [https://arxiv.org/abs/1607.00653]
  
• Case study & code: [https://medium.com/analytics-vidhya/analyzing-disease-co-occurrence-using-networkx-gephi-and-node2vec-53941da35a0f]
  

The algorithms above are only small portions of 2vec-style models. And if you are interested, I think this website may help you.

Summary:

In the context of machine learning, embedding functions as a task-specific dictionary. It encodes our targets with a series of numbers that serves as a unique ID. We like to use embedding because it can help transform the discrete, categorical variables into model-readable data, and it can also help reduce the data’s dimensionality and complexity. I also listed several selected 2vec-style models.

---

---